Optimization problems are notoriously tricky and fun to solve.  Examples include finding the best route to deliver packages across a busy metropolis, laying out a store to maximize sales, or mining crystal deposits before an alien invasion.  For this challenge, we're giving you a new take on optimization problems that require balancing budget, time, and space.

For this challenge, you must build an algorithm that solves for the most profitable solution by sending workers to collect Rewards over a map area within a particular time and budget.  There are several rules that your solution must factor in, which are discussed below. 

You can start this challenge in two ways.  If you are new to optimization problems or want an easy warm-up, check out the Sandbox version of the challenge (link), otherwise stay here.  Both contain the problem space and rules but different levels of complexity.  Solutions for the Sandbox model won't be considered for the full challenge.

The Problem Space

There are five elements to balance when building a solution:

• Maximizing the amount of Rewards extracted.

• Hiring the right amount of Workers to collect Rewards.  

• Accessing the Graph where Rewards are distributed in the most efficient manner.

• Staying within a budget of $800,000.

• Completing the work within 40 time steps.

The goal is to maximize the Profit (Total Reward Extracted - Total Costs) by hiring the right amount of Workers to collect as many Rewards across the Graph within the given time. Let’s discuss each element in more detail.

The Graph can be considered a map where the Workers navigate to collect Rewards (Figure 1). The Graph is a randomly distributed set of nodes and edges. Each node, or site, can either be empty or contain a Reward. Workers travel along edges to access different sites to extract Rewards. There is one unique site, the Origin, where all Workers start from.

Rewards can be considered minerals, tomatoes, Bitcoin, etc., that Workers collect. Rewards are not the same as Budget. Some sites contain higher value Rewards than others and take more time to acquire those Rewards: 

• Type 1 sites (red) have a low Reward value and can be acquired in a few time steps.

• Type 2 sites (blue) have a medium Reward value and can be acquired over more time steps.

• Type 3 sites (green) have the highest Reward value but take the longest number of time steps to acquire. 

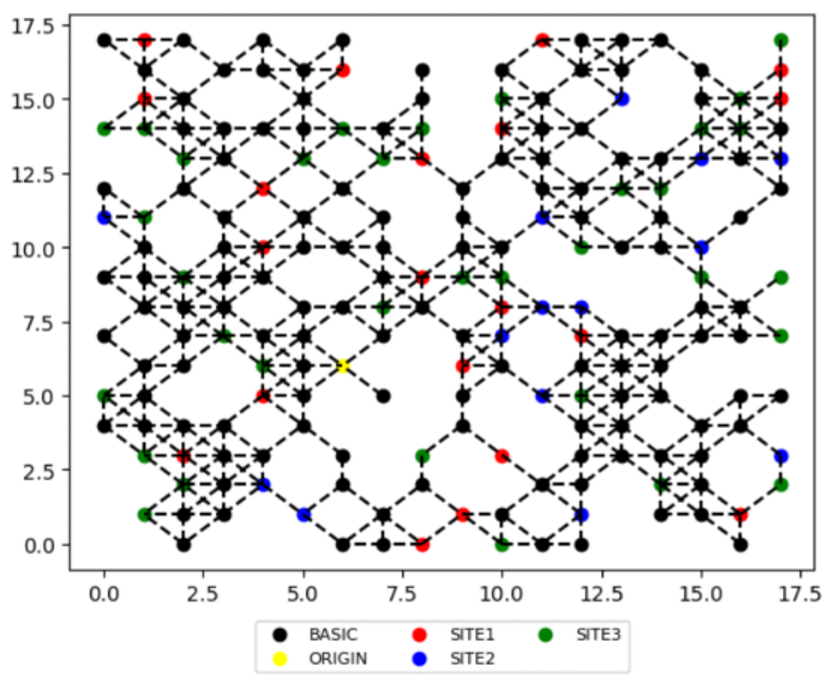
Figure 1: Test Graph that your algorithm must navigate to find the most profitable path for Workers.

Workers can be thought of as drone chile harvesters, miners of the Klondike Gold Rush, or any other clever analogy you want to imagine. Workers are hired to do the Reward extracting and have a cost for each time step. Your Budget is the only limit to the number of Workers you can hire. Just like Rewards, there are three different types of Workers. Worker types have different time step rates and extracting rules:

• Worker 1 Type costs 100/step and can only extract Type 1 sites.

• Worker 2 Type costs 600/step and can extract Type 1 and Type 2 sites.

• Worker 3 Types costs 2,000/step and can extract Types 1, 2, and 3 sites.

Workers can only move one unit per time step. However, Workers can use sites indefinitely (backtrack, travel while another Worker is on-site extracting). 

The Budget and time limit are self-explanatory. A solution must stay within the Budget when hiring Workers. Rewards cannot be added to the Budget. A solution can only operate for 40 time steps. Investigate the Starter Notebook for more details about Rewards, Workers, and the graph.

While these rules are straightforward, only an efficient algorithm can find the best path to maximize profit. For example, a single Worker 3 Type on the Test Graph has more possible paths than the number of cells in a brilliant human data scientist, which you are.

Build Your Own Training Data

We wanted to give participants the option to explore this problem and progressively build a solution. To enable this, we have published the Lyra Graphtool package that allows you to build your graph. Please use this package to explore the problem further. One strategy could be to build your algorithm and test it on the two small Train Graphs provided in the Data Tab.  Then use the Lyra Graphtool to build more complex graphs to optimize your algorithm for the Test Graph on this page and for final evaluation. The Lyra Graphtool is a big package but some of the elements that you can experiment with are:

• Style - random or grid

• Size of Graph

• Number of Sites and Their Types

• Time Steps and Budget

The Starter Notebooks allow you to walk through all the different parameters for building a graph and preparing your algorithm to win. You can also consult our GitHub Docs Site for more information.

Evaluation

Submissions for the challenge are your proposed best path to maximize profit (Total Reward - Total Budget) on the Test Graph. The Live Leaderboard scoring algorithm is the total profit of the path you submit.  The Lyra Graphtool has built in functions to export your best path and to calculate profit.

Final Evaluation

At the end of the challenge, Xeek will request the models from the users in the top 10 Live Leaderboard positions for review by a panel of judges.  The Judges will run a submitted algorithm ten times on a complex holdout map, and each run will be given 2 hours on a SageMaker ml.g5.8xlarge instance. The top Profit score from each of those ten runs will be averaged and used for 95% of the users final score.  

The remaining 5% of the final score will assess submissions on the interpretability of their submitted Jupyter Notebook. The interpretability criterion focuses on the degree of documentation (i.e., docstrings and markdown), clearly stating variables, and reasonably following standard Python style guidelines. 

A submission must contain a Jupyter Notebook, a requirements.txt, and any additional parameters a contestant has generated. The Jupyter Notebook must include code that saves a JSON file generated by the Configuration class object containing your optimal solution - use its class method save_to_json. Do not change the args in the Lyra Graphtool package when building your solution. Final submissions that have changed the args will be rejected. All custom arguments should be self-contained and invisible to our Judge’s execution of your submission. The requirements.txt should describe the environment used to generate the model. It must contain the libraries and their versions, and the Python version (>=3.6 is preferred). See the Starter Notebook on the Data Tab for an example.

Prizes

Prizes will be awarded for first ($26,500), second ($16,000), and third ($10,500).  Participants with scores in fourth through tenth places will receive $1,000 for their valid submission.